リーマン級数は微積分学のカギである・・・
無限、∞は夢幻の彼方・・・
よって、リーマン級数で展開して、現実的な計算を行う - チューリング・マシン
チューリング・マシンは仮想機械である・・・
第二の月、空転金融原子炉の炉心でもある・・・
鳩山さんは数理工学専攻、バーチャル、よって、浮世離れする => ゲーム屋さん
志位さんは物理工学専攻、リアル、よって、現実的である => プラグマティスト
そのかけ橋が計測工学、リアルワールド(物理世界)をコンピュータでシミュレート(仮想世界)する
東大応用物理系学科は?
数理工学専攻、計測工学専攻、物理工学専攻のみっつに分派する・・・
だが、応用物理学の基礎を学ぶので、これらみっつの専攻の基礎的な素養は身につく・・・
シミュレーション技術は、プランの策定、および、結果の予想、つまり、成果の予想にとって、重要な技術である・・・
---Wiki

複素数平面におけるリーマンのゼータ関数。点
s における色が ζ(
s) の値を表しており、濃いほど 0 に近い。色調はその値の偏角を表しており、例えば正の実数は赤である。
s = 1 における白い点は
極であり、実軸の負の部分および臨界線 Re(
s) = 1/2 上の黒い点は
零点である。
数学におけるリーマンゼータ関数(-かんすう、Riemann's zeta function)とは、
で表される
関数のことをいう。素数分布の研究をはじめとした解析的数論における重要な研究対象であり、数論や力学系の研究を始め数学や物理学の様々な分野で用いられているゼータ関数とよばれる一連の関数のうち、最も歴史的に古いものである。
リーマンのゼータ関数ともよばれる。
とも定義できる。
すでに
オイラーがこの関数を考察しておもに特殊値に関する重要な発見をしていたが、のちにより重要な貢献をした
リーマンがもちいたギリシャ文字のζによる表記にちなみリーマンゼータ関数と呼ぶ。上記級数は
s が 1 より大きい
実部をもつ
複素数のときのみ収束するが、
解析接続によって1を除く
複素数平面の全域で定義された
有理型関数となる。
s = 1のとき上の表示は
調和級数となり、無限に発散する。
ゼータ関数に整数を代入したものをゼータ定数またはゼータ関数の特殊値と言う。任意の正の偶数2nについて
と表せる。ここで、
B2nは
ベルヌーイ数である。また、
n ≥ 1の時、
が成り立つ。
s が負の偶数であれば ζ(
s) = 0 であり(算出は
フーリエ級数参照)、これらをリーマン・ゼータ関数の
自明な零点とよぶ。これらの表示はオイラーによる。
具体的には、
が成り立つ。 ここで、
とおくと、
s が正の奇数のときの ζ(
s) を表す簡潔な表現は得られていない。それでも
ラマヌジャンなどは次のような表示式を得ている。
小さい正の奇数については、
などが数値的に成り立っている。
これらに関して、
という級数が知られている。
アペリーの定理によるとζ(3)は無理数である(1978年,ロジェ・アペリ)。
オイラー積 [編集]
ゼータ関数と
素数との最初の関連はオイラーによって示された。すべての素数
p をわたる
無限積によってリーマンゼータ関数は
という表示を持つ。これを
オイラー積あるいは
オイラー表示という。この無限積が Re(
s) > 1のときゼータ関数に絶対収束していることは、
幾何級数(等比級数)の公式
が絶対収束すること(特に有限和のように
分配法則が成り立つこと)に注意して、十分に大きな素数
p' を固定し、それ以下の素数
p にを亘る有限積をつくり、その
p' → ∞ とした極限を考えることで示すことが出来る。この部分有限積の展開について、自然数
n の
素因数分解に現れる最大の素因数が
p' であれば、そこまでの有限積の中に
n が含まれるため、上のようなゼータ関数のオイラー積表示が成り立っている。
ゼータ関数の表示と関数等式 [編集]
ゼータ関数は次のような表示ももつ:
ここで ρ に関する積はリーマン・ゼータ関数の複素零点全体をわたるものとする。この式から、
という式を推測している。
という関数方程式を持つことが示された。ここでΓは
ガンマ関数である。これは複素解析的関数の
解析接続がはじめて明示的におこなわれた例である。 s = -2
n(nは自然数)を代入すると
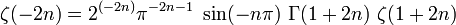
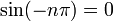 なので
なので 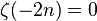 である。したがって-2n はゼータ関数の零点である。
である。したがって-2n はゼータ関数の零点である。
次のように修正されたゼータ関数(これは実質的にリーマンによって導入され、完備化されたゼータ関数と呼ばれる)
は s と 1 - s に関する以下のような対称的な関数等式をもつ:
ゼータ関数と数論的関数 [編集]
ゼータ関数を適当に組み合わせることにより、様々な数論的関数を係数とする
ディリクレ級数の母関数を得ることができる。
と表せる。この式と
ζ(2) の値から、分布が
一様であるという仮定のもと、任意に取り出した二つの整数が
互いに素である
確率は 6/π
2 であることが証明できる。
自然数
n の(正の)約数の個数を
d(
n), すべての約数の和を
σ(n) で表すとき、
が成り立ち、また、
n と互いに素な
n 以下の自然数の個数を
オイラーのφ関数 φ(
n)で表すとき、
なども成り立つ。
ゼータ関数と素数の個数関数 [編集]
以下に素数分布、すなわち素数の個数関数 π(x) とゼータ関数との関係をのべる。
まずゼータ関数のオイラー積表示の両辺において対数をとり、
テイラー展開で和の中の対数を展開する:
ここで各 n ≥ 1 について
と変形して、先の式に代入すると
通常
と置いて、最終的に上式は次のように書かれる。
この公式に、
メリン変換などと呼ばれる積分の反転公式を使うと、Π(
x) を表示する公式を求めることができる。この公式は、
リーマンの素数公式、あるいは
明示公式(explicit formula)などと呼ばれている。なおメビウスの反転公式によって π(
x) は
とかけることを注意しておこう。
ゼータ関数の零点の分布に関する未解決問題であるリーマン予想は、素数公式の近似精度に関連している。この予想は純粋数学におけるもっとも重要な未解決問題であると考える数学者は多い。
---Wiki
チューリングマシン (英: Turing Machine) は計算模型のひとつで計算機を数学的に議論するための、単純化・理想化された仮想機械である。

仮想機械の実装方法は、以下のいずれか、あるいは組み合わせなどがある。
仮想機械は通常は、ユーザーやプログラムから「別のコンピュータ」に見えるもの(複数のOSまたはOS環境を実現するもの)を指すが、コンピュータの初期には、
仮想記憶や
マルチタスク、
マルチユーザー、
タイムシェアリングなど、現在では一般的なOSの機能となった技術を含める場合がある。仮想機械の技術は
メインフレームで生まれ発展したが、現在は各種
サーバでも一般的な技術となりつつある。
利点と難点 [編集]
実現方式にもよるが一般的には、仮想機械の利点・難点には以下が挙げられる。
- 利点
- 多数のユーザーやプログラムが、独立して平行使用でき、相互に干渉しない(信頼性、可用性)
- 別のアーキテクチャのOSやソフトウェアが使用できる(互換性)
- 個々の仮想機械の追加・変更・削除が容易、ハードウェアの集約、負荷の平準化(運用容易性、サーバ統合)
- 難点
- 性能が犠牲となる(仮想化のオーバーヘッドを見込んだハードウェア性能が必要)
- 構成・運用が複雑になる(一定のスキルが必要、特に障害時の問題判別時)
- 稼動させるプログラムや周辺機器の、サポートやライセンスに制限がある場合が多い
歴史 [編集]
メインフレーム [編集]
ハードウェアによる仮想化 [編集]
1964年 IBM System/360は、同様に既存の
IBM 1401や
IBM 1620の命令セットをマイクロコードでエミュレーションした。また、コンピュータ・アーキテクチャを定義し標準化し、以後の上位互換性を提供した(通常は仮想化と呼ばれないが、プログラムから見れば一種の仮想機械と言える。この効果として、メインフレームでは
アセンブリ言語でもバイナリでも、40年以上経過した現在まで上位互換が続いている)。
1973年 IBM System/370モデル158およびモデル168により、物理分割(
PPAR)をサポート。単一のコンピュータとしても、複数のコンピュータとしても使用可能。ただし細かいリソースの割り当てはできず、変更にはコンピュータ全体の再起動が必要。
IBMのPR/SMに相当する機能には、
日立製作所 PRMFなどがある。
仮想化OSによる仮想化 [編集]
OSによるリソースの仮想化 [編集]
マルチタスク(アプリケーションによるマルチプログラミングではなく、OSの機能によるマルチタスク)は商用では、
OS/360のバリエーションのひとつであるMVTと、後継の
MVSで登場し、広く普及した。入出力待ちなどにCPUが他の処理を行えるため、処理の
応答時間短縮と全体の
スループット向上がもたらされた。
なお、メインフレームにおけるこれらの「マルチタスク」は、単に複数のプログラムが同時に動かせるというだけではなく、複数の独立したアドレス空間(リージョン)を作成し、ハードウェアの機能も使用して完全に分離し、同時稼働するプログラム同士は直接見えない(バグや悪意あるプログラムでも相互に干渉できない)ものである。この点では、後の各種
UNIXや
Windowsなどの「マルチタスク」と比較すると、「仮想機械」に近いレベルのもので、
可用性や
セキュリティも向上した。同様の仕組みは
2009年現在、MVSの後継の
z/OSの他、IBM
z/VSE、富士通 MSP/XSP、日立製作所
VOS3 などでも採用している。
タイムシェアリング(時分割多重)による並列処理(マルチユーザー)は、アプリケーションプログラムやユーザーに、複数のコンピュータを同時使用するイメージをもたらし、
オンライン・
リアルタイム処理の普及をもたらした。なお、マルチタスクとタイムシェアリングは別の技術であるが、現在では組み合わせて使用されている。(上記のMVSなどでは、マルチタスク環境の一部で、タイムシェアリング環境を稼働させ、それによりマルチユーザーを実現している。またマルチタスク自体も、初期には入出力待ちによる
割り込みが基本であったが、現在ではタイムシェリングによる割り込みを併用している。)
ミッドレンジ [編集]
1979年 IBM System/38は、TIMI(Technology Independent Machine Interface、技術に依存しないマシンインターフェイス)を採用した。TIMIは、メインフレームで採用されたマイクロコードによる互換性確保を更に進めたもので、主に水平型レベル・マイクロコードにより実現され、ハードウェア・アーキテクチャ(CPU命令セット等)とプログラムを分離している。プログラムの配布は中間コードであるバイトコードで行われ、インストール時にハードウェアの命令セットに展開される。このためソースプログラムを配布すること無く、実行時の性能を犠牲にすることもなく、別のアーキテクチャのハードウェアへの移行も容易である。実際、
CPUアーキテクチャの移行(独自CISC→POWER)も容易に行えたとされる。
商用UNIX [編集]
商用UNIXベンダーによる仮想化技術には以下がある。現在の仮想化技術は各種のハードウェアとソフトウェアが密接に連携しており、またベンダーにより各技術の範囲が異なるため、ベンダー単位に記載する。
- SUN N1構想(Unified Virtualization Manager Environment)
- DSD (Dynamic System Domain) - 物理分割。動的なリソース移動も可能。上位機種のみ。
- LDOM (Logical Domain) - ファームウェアによる論理分割。複数OSを稼働。上位機種のみに提供予定。
- Solarisコンテナ - OS(Solaris 10)の標準機能。アプリケーションから見て複数のOS環境(インスタンス)を提供。
- Solarisリソース・マネージャ - ミドルウェアの機能でアプリケーションのワークロードを制御
- HP Virtual Server Environment (VSE)for HP-UX
- nPartitions(nPars) - ハードウェアによるパーティショニング技術
- Virtual Partitions(vPars) - nParをさらに分割できる論理パーティション技術、1プロセッサ単位で構成
- HP Integrity Virtual Machines (Integrity VM) - 各パーティションにプロセッサ・リソースを5% - 100%の範囲で動的に割り当てる、柔軟なsub-CPUパーティションニング技術 。
- HP-UX Workload Manager - パーティショニング、クラスタ、ユーティリティ・プライシングと連携し、サービスレベル維持に向けた リソース割り当てを自動化 。
UNIX/Linux/Windowsなど [編集]
仮想化OS [編集]
仮想化OS(仮想マシンモニタ)は、一つの計算機資源を複数の計算機資源としてハードウェア的に利用したり、物理的資源を区分けして特定のワークロードがシステム全体を独占させない目的(パーティション)の為に作られたもので、
VMware、
Xen、
Oracle VM(ベースは
Xen)、
Hyper-Vなどがある。
一台のコンピュータを複数のコンピュータとして、ハードウェアレベルで使うことができる。一台のコンピュータ上で特に
オペレーティングシステムの変更なしに、複数のゲストオペレーティングシステムを稼働させたりする。稼働させる複数のゲストオペレーティングシステムは、全く別の種類のオペレーティングシステムであることも可能である。
元々仮想マシンモニタは
メインフレームにおいてその資源を各ワークロードの負荷に応じて動的に分割し、システム全体の利用効率を上げるために用いられた。計算機が高性能化した現在では、小規模なWebサイトホスティングのような軽い処理を一般的なサーバでも仮想マシンモニタを用いて並列に実行し、資源の有効活用することが行われている。
- → ハイパーバイザも参照
OSの機能 [編集]
CPU [編集]
言語環境による仮想機械 [編集]
これらの仮想機械の目的は、物理
命令セットアーキテクチャと、論理命令セットアーキテクチャの分離にあり、一度コンパイルされたプログラムは物理命令セットアーキテクチャが何であれ、仮想機械によって実行する事ができる。またJavaのようにハードウエアや
オペレーティングシステムを抽象化し、オペレーティングシステムを含むコンピュータアーキテクチャ自体を隠蔽し、あらゆるシステムで動作するプログラムの設計を可能とする事を目的とした物もある。
x86アーキテクチャにおける
x86-64のように、物理命令セットアーキテクチャはプロセッサの進化に伴い変更される。適切に設計された論理命令セットアーキテクチャは、これらの物理命令セットアーキテクチャの進化の恩恵を受けつつ後方互換性を維持できるので、既存プログラムの保守コストが低減される。
また、論理命令セットアーキテクチャを固定することで、
コンパイラに対して複数の物理命令セットアーキテクチャに対応したコードジェネレータを都度開発しなくて済む。また、非常に複雑で多岐にわたる物理命令セットではなく、その言語や環境にあわせて洗練された命令セットに対応したコードジェネレータを一回だけ設計すれば良く、コンパイラ開発における負担を大いに軽減する。
なお、言語による仮想機械をハードウェア化したものとして以下がある。
- Pascalのp-codeインタプリタはウェスタン・デジタル MCP-1600チップセットが作られた
- Javaでは、サン・マイクロシステムズがJavaバイトコードをネイティブに実行するプロセッサを製作する計画を発表したが、実際にはそのサブセット的実装にとどまった。
- ARMアーキテクチャの中にはJazelleと呼ばれるJavaバイトコード実行モードに切り換える事ができるものがあり、Java仮想マシンの裾野を広げている。

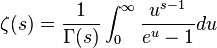

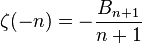
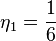
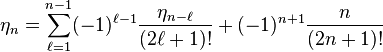
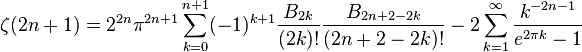


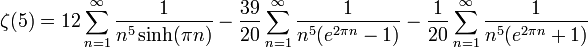


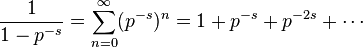

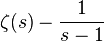
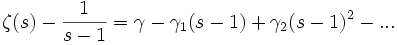

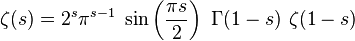
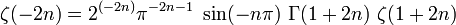
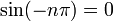 なので
なので 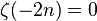 である。したがって-2n はゼータ関数の零点である。
である。したがって-2n はゼータ関数の零点である。




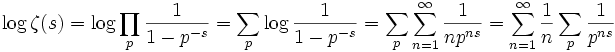

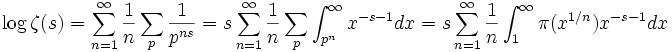

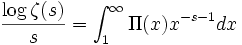




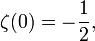
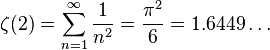 (→
(→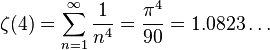

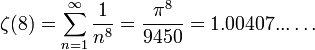
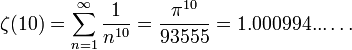


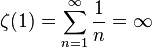 (→
(→ (アペリー定数)
(アペリー定数)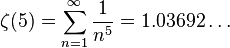
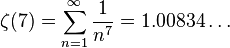
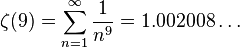
0 件のコメント:
コメントを投稿