AH Tokyo 検索

カスタム検索

10/06/2010

リーマン予想？　懸賞問題（BS hi)

多項式時間で解ければ、計算可能？　つまり、現実的な計算の可能性を問うているのでは？


複雑系システム、非線形システムなどのモデリングには重要なコンセプトである・・・



オイラー展開、リーマン展開は、

微積分の近似値を代数方程式で表現する？　数列で表現する

つまり、近似値の現実的解法である・・・

よって、彼らの業績により、コンピューター計算学が進展した　－　NP困難


じゃ、ないのかな？　－　昔の大学生

なるほど、素数に関係しているのか・・・

素数の算法も、計算機科学にマッチするように・・・

ふるいにかけて、素数を求める？　－　計算機科学？



---Wiki



NP困難（-こんなん、NP-hard）とは計算複雑性理論における問題のクラスの1つ。非形式的に言えば「NPに属する最も難しい問題と比べて、少なくとも同等以上に難しい」問題である。問題 H がNP困難のクラスに属するとは、「NP完全問題に属するいずれかの問題 L が H へ多項式時間チューリング還元可能である」と定義される。即ち\scriptstyle L\, \leq\,_T Hであり、NP困難問題を解ける神託機械がもしあれば、それを利用してNP完全問題を多項式時間で解くことができる。
NP完全問題とは、NPの任意の問題から多項式時間多対一還元可能であり、かつ、NPに属する問題である。これと異なり、NP困難である問題はNPに属するとは限らない。PやNPは決定問題のクラスなので、NP完全もまた決定問題に限られるが、NP困難には決定問題、検索問題(en)、最適化問題など様々な問題が属しうる。
上に挙げた定義から次のことが言える（以下は定義ではなく主張）。
  • 問題 H は少なくとも L と同等以上に難しい。なぜなら H を用いて L を解けるからである。
  • L はNP完全であり、NPの中では最も難しいので、問題 H は少なくともNPと同等以上に難しい。しかし H はNPに属している必要はなく、したがって決定問題ではなくても良い。
  • NP完全問題同士は互いに多項式時間多対一還元（別称：多項式変換とも）可能なので、すべてのNP完全問題は H に還元して多項式時間で解ける。したがってNPに属する全ての問題も H に還元できる。ただし、ここでは二種類の変換を組み合わせていることに注意が必要。NP完全に属する決定問題をNP完全な問題 L に帰着する際は多項式変換であり、L を H に変換する際は多項式時間チューリング還元である。
  • もし最適化問題 H の特殊例としてNP完全な決定問題 L を考えられるなら、H はNP困難である。
  • もし H がたまたまNPに属すなら、H はNP完全。なぜならこの場合多項式時間チューリング還元が多項式変換の要件を満たすので。[1]
NP困難な最適化問題は、最適解を求めるのが非常に困難であるため、近似アルゴリズムに関しても研究されている。

P≠NP予想との関係 [編集]

もし、いずれかのNP困難な問題を多項式時間で解くアルゴリズムが存在したなら、NPの全ての問題について多項式時間で解けることになり、P = NP が成り立つ。同様に、いずれかのNP完全な問題を多項式時間で解くアルゴリズムが存在した場合も、NPに属する全ての問題が多項式時間で解ける。そのため「いずれかのNP困難（またはNP完全）な問題を多項式時間で解く方法が存在するか」という問題はそのまま P≠NP予想の否定の証明になる。ところが、P＝NPが成立しても「任意のNP困難な問題が多項式時間で解ける」とは言えない。これに対し、P≠NPが成り立つならば「いかなるNP困難な問題についても、これを多項式時間で解く一般的なアルゴリズムは存在しない」と言える。この関係を右上のベン図に示す。

NP困難な問題の例 [編集]

別定義 [編集]

NP困難の別定義として、NP困難を決定問題に限定し、チューリング還元の替りに多項式時間多対一還元を用いるものがある。この場合、問題 L がNP困難であるための条件は\forall L^\prime\in \mathbf{NP}, L^\prime \leq_p L\!である。ここでもし L が NP に属すなら、L はNP完全。

NP関連クラスの命名規約について [編集]

NPに関連するクラスの名称はまぎらわしい。「NP困難」はクラス名に「NP」と付くのに、全てがNPというわけではない。しかし現状では定着した名称なので、いまさら変わりそうにない。とはいえ、NPを中心に置いた上でそれなりに体系があるのも事実である。
NP完全
NPの中では「完全」な問題を意味する。つまりNPの中では最も解くのが難しい。　
NP困難
「少なくとも」NPと同等以上に難しい問題（ただし、NPに属するとは限らない）。
NP-easy
「たかだか」NPと同等以下しか難しくない問題（ただし、NPに属するとは限らない）。
NP-equivalent
NPと同等に難しい問題（ただし、NPに属するとは限らない）。

関連項目 [編集]

  • NP完全問題
  • 多項式時間変換 - 多対一還元やチューリング還元に計算時間の制限を付加したもの。
  • チューリング還元 - 計算時間を多項式時間に制限する場合は、それを示すために前に「多項式時間～」と付けるか、または Cook還元と呼ぶ。
  • 多対一還元 - 計算時間を多項式時間に制限する場合は、それを示すために前に「多項式時間～」と付けるか、または Karp還元と呼ぶ。単に「多項式変換」と書けば通常 Karp還元を指す。












---Wiki

リーマン予想（リーマンよそう、Riemann Hypothesis）とは、ドイツの数学者ベルンハルト・リーマンによって提唱された、ゼータ関数の零点の分布に関する予想である。英語表記 Riemann Hypothesis の直訳であるリーマン仮説と表記したり、RHと略すこともある。数学上の未解決問題のひとつであり、クレイ数学研究所はミレニアム懸賞問題の一つとしてリーマン予想の解決者に対して100万ドルの懸賞金を支払うことを約束している。



リーマンは素数の分布に関する研究を行っている際にオイラーが研究していた以下の級数をゼータ関数と名づけ、解析接続を用いて複素数全体への拡張を行った。
ゼータ関数を次のように定義する。
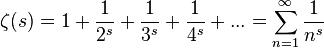
\zeta(s)=1 + \frac{1}{2^s} + \frac{1}{3^s} + \frac{1}{4^s} + ... = \sum_{n=1}^\infty \frac{1}{n^s}
1859年にリーマンは自身の論文の中で、複素数全体 (s≠1) へゼータ関数を拡張した場合、
ζ(s) の自明でない零点sは、全て実部が1/2の直線上に存在する。
と予想した。ここに、自明な零点とは負の偶数（-2, -4, -6, …）のことである。自明でない零点は0 < Re(s) < 1[1]の範囲にしか存在しないことが知られており（下記の歴史を参照）、この範囲をクリティカル・ストリップという。
なお素数定理はリーマン予想と同値な近似公式[2]からの帰結であるが、素数定理自体はリーマン予想がなくとも証明できる。この注意は歴史的には重要なことで、実際リーマンがはっきりとは素数定理を証明できなかった理由はリーマン予想の正否にこだわっていたためであると思われている（素数分布とのゼータ関数との関係はゼータ関数や素数定理、リーマンの素数公式の項を参照のこと）。
現在もリーマン予想は解かれていない。数学における最も重要な未解決問題の一つである。リーマンのゼータ関数を特殊な場合に含むL関数に対しても同様の予想を考えることができ、これを一般化されたリーマン予想（Generalised Riemann Hypothesis：GRHと略される）と呼んでいる。
最近では、虚部が小さい方から10兆個（X. Gourdon and P. Demichel,2004）までの複素零点はすべてリーマン予想を満たすことが計算されており、現在までにまだ反例は知られていない。現在では多くの数学者が（当然のことだが、はっきりした根拠を持たずに）リーマン予想は正しいと考えているようである。しかし無限にある零点からみればたかだか有限の数表などは零点分布の真の姿を反映するには至らないとして、この計算結果に対して慎重な数学者もいる。歴史上有名な数学者の中でもリーマン予想を疑っていた数学者はいる[3]。

リーマン予想の歴史 [編集]




以下の各命題は、リーマン予想と同値である。
  • 十分大きな任意のxに対し、

    |\pi(x) - {\rm li}(x)| \leq C\,\sqrt x\,\ln(x)
    が成り立つような定数 C が存在すること[7]。ここに li(x) は対数積分を表す。これは

    \pi(x)={\rm li}(x)+O(x^{1/2+\epsilon})\,
    と表現しても同じことである。ただし、O はランダウの記号である。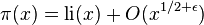
  • 自然数 n の正の約数の和を σ(n)（約数関数）表すとき、n > 5040に対して

    \sigma(n) < e^\gamma n \ln \ln n \,
    が成り立つこと[8]。ここにγはオイラー定数を表す。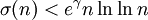
  • 任意の自然数nに対して

    \sigma(n) \le H_n + \ln(H_n)e^{H_n}
    が成り立つこと[9]。ここにHnはn番目の調和数、すなわち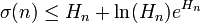

    H_n=\sum_{k=1}^n \frac{1}{k}
    で定義される有理数である。

投稿者 時刻:
ラベル:

0 件のコメント:

コメントを投稿

登録: コメントの投稿 (Atom)

The Definition Of Art Harbour Blog



The Definition Of Art Harbour


Virtual International Trade Harbours Of Art


Opening Anniversary Date: December 1, 2006

Language: Multi Language


Each harbour can export the works toward the virtual world.

People and organization can import the works from all over the world.


Now,Item: Works on Art Activities that are expressed with Photos and Explanations etc.

Export Method: Each Harbour put the Works onto this blog

Import Method: People and Organizations accsess this blog

Order Method: People and Organizations put some comments about the Works onto this blog.


In the future, we will need transportation including trains,airplanes,ships, cars, buses etc.

in order to export and import people, goods etc. ?


Art Harbour


アート・ハーバーとは


アートのバーチャル国際貿易港


開港記念日：2006年12月1日

言語：マルチ言語


各港は、バーチャルな世界へ向けて、作品を輸出できる

人や組織などは、バーチャルな世界から、作品を輸入できる


現時点輸出品目：　アートに関する活動などを「写真と文などで表現した作品」

輸出方法：　各港で作品をこのブログに書き込むことで、輸出したものとみなす

輸入方法：　人や組織が作品をこのブログで参照することで、輸入したものとみなす

注文方法：　感想などをコメントに入れることで、注文したものとみなす


将来、、、列車、飛行機、船、車、バスなどを利用して、リアルな人や物が輸出入できる？


アート・ハーバー

Multi Language

現時点では？


ブログは日本語ベース


Google Translatorで、各国語へ、変換




そして、現場で、リアルなコミュニケーションは？


英語ベースで、現地語がお愛想・・・


こんな感じかな？


Aoyagi YoSuKe

Art HarbOur


The Gaiaと各ハブは？


英語がベースで、Google Translatorで、各国語へ・・・

Copyright and Responsibility of AH Shimokitazawa blog



Copyright:


Each manager or each member of Each AH Local must independently handle Copyright.


Each may insist on Copyright or discard Copyright independently.


Copyright depends on each manager or each member.


Responsibility:


Each manager or each member of Each AH Local

must independently have the resposibility on the posted works.

Art Harbour Shimokitazawa


コピーライト：

各アート・ハーバーのマネージャーまたはメンバーは

各々でコピーライトの取り扱いをしなければならない。

コピーライトを主張するか破棄するかは各々に任される。


責任：


各アート・ハーバーのマネージャーまたはメンバーは

各々が投稿した作品に関して責任を持たなければならない。


アート・ハーバー 下北沢


Posting Rule - 掲載ルール




Introducing People, Works, Shops etc. related to Art Harbour as a spot ad.


As a general rule, the details such as map, price should be in the Official Sites related to the ad.

Each ad may contain the Official Sites' URL related to the ad.


Restriction: The Number of Photos is within 6（basically 3). about 640x480 pixel


Ad Size: Within about 2 standard printing papers.


Example: Spot ad. , Flyer, Live Report, Poem, Short Story, Illustraltion, Photo, Paintings etc.


Art Harbour Shimokitazawa



アート・ハーバーに関連した人、作品、店などをスポット広告として紹介する。


原則として、地図や価格などの詳細は広告に関連したオフィシャル・サイトに掲載する。


各広告には関連オフィシャル・サイトのURLを掲載しても良い。


制限：写真など6枚以内（基本は3枚） 1枚に付き640×480ピクセル程度


サイズ：標準プリント用紙（A4）約2枚以内


例：スポット広告、フライヤー、ライブの報告、詩、イラスト、絵など



アート・ハーバー　下北沢