早すぎたノーベル賞
パウリ、朝永振一郎
彼らは異端だった・・・
今や、パウリ、朝永が主流になりつつある・・・
賞の価値とは? 評価システムの価値でもある・・・
どうでもいいが・・・ 日本人は価値が分からないので、賞に頼る
官僚主義、権威主義に陥って、学問の生産性が大幅に低下してしまった
ブレイクスルーを起こせない・・・ どうしようにもならない・・・
break through
【句動-1】〔敵・難関などを〕打ち破る
【句動-2】〔困難などを〕切り抜ける
【句動-3】〔研究者などが〕大発見をする
【句動-4】〔太陽・月が〕雲間から現れる
【句動-5】〔隠れていた物・本音などが〕現れる
【名】<→breakthrough>
僕は数学者じゃないので、このような各論になると・・・
頑張ってね~~~、あんたのお仕事・・・
個人的には逆だと思うが・・・
E=MC2が一般相対論(適用範囲が広いが、近似値である)
偏微分方程式で表現するモノこそ、各論の特殊相対論だと思う
そういう意味では?
ニュートンのプリンキピア、古典力学こそ、一般的な原則である、近似値であるが・・・
現代物理はその各論であると考えている・・・
だから、ニュートンは、現代物理の元祖である・・・
ニュートンはみっつの方程式で、宇宙のフレームワークを記述した、驚異的である・・・
ここで、また、アマルガメイション合金の法則
クリエイティブの原点は料理である
Webの世界から、Bioの世界へ・・・
料理のベースこそ、ダシである・・・ 基本である
和風 かつを節、昆布、煮干し
フランス ソース
韓国 ジャン、タレ
・・・
・・・
・・・
ダシをベースにして、料理がある・・・
宇宙空間は? 6次元、11次元 => 数学者はゲーム、バーチャル
物理学者は? 四次元時空、じゃあ、電磁場と重力場を加えて、6次元空間とする
電場と磁場を区別して、四次元時空+電場+磁場+重力場で表現する・・・
何でもいいが、宇宙はリアルである - 物理学者
個人的に考えるには? 三次元空間(電磁場+重力場)+時間、すなわち、四次元時空・・・
空間が何か? これは、難しい・・・
極論は?
宇宙はエネルギーである、エネルギーの不可逆遷移過程である
時間はエネルギーの遷移単位である・・・ 存在はエネルギーの現れ方、フェノミナである・・・
そんな感じになってしまう・・・
空間って、何? 時間って、何? 存在って、何?
物理学はギリシャ哲学に端を発する・・・
宇宙の形? 形って、何?
形を言うなら、その前に、上の三つが何であるか?
それが分からなければ、形の意味がない・・・
認知科学、人は何を認知しているのだろうか?
認知科学、脳科学を抜きに、形は語れない・・・
人は地球の重力場に支配されている
よって、鏡の像は左右が逆だが、上下は逆にならない・・・
形を語るトキ、人が重力場に支配されていることを忘れては意味がない
意味が分かるかな?
簡単に言えば、ムリ数を宇宙の果てまで、書いて言っても、ムリ数は続いて行く
つまり、人が作った算数の仕掛けの延長でしかない・・・
五芒星はムリ数で表現されている・・・
9/08/2010
西の壁は?
ソロモン王とシバの女王の争い?
東の壁は?
大英帝国発、ケインズとマルクスの争い?
じゃないのかな?
争いの本質は?
嘆きの壁と、板門店・・・
東西の壁・・・
AO
五芒星もひとつの光芒は72度。なのだが、黄金比に無理数を組み込んだ・・・ たぶん、ここいら辺りが魔法のランプや空飛ぶ絨毯の謎だろう・・・
五芒星と黄金比

図において、赤の線分と青の線分の長さの比、同じく青と緑の比、緑と紫の比は一定の値
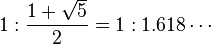 を取る。 これは黄金比と等しい。
を取る。 これは黄金比と等しい。
古くから黄金比で構成されている図形は美しいとされており、単純ながらも黄金比を数多く含む五芒星は美しい図形の代表格とされた。
黄金比・・・ 割り切れない・・・ 不安定・・・
ダビデの星(
六芒星)と五芒星
---Wiki
ナチス・ドイツによる
ホロコーストにおいて、
ユダヤ人は、
黄色で描いたこの星型紋様(
独:
Judenstern=
直訳でユダヤの星と呼ばれていた。当時は
独:
Davidstern=ダビデの星とは表記していなかった)をつけさせられた。
数学はゲームである、リアリティから、外れてしまった・・・
残念です・・・ 宇宙の形の可能性が8つのパターン
ほとんど無意味です・・・
ガウスに戻ってね・・・
---Wiki
数学の、特に
確率論や
統計学で用いられる
正規分布(
せいきぶんぷ、
英語:
normal distribution)または
ガウス分布(Gaussian distribution) とは、
平均値の付近に集積するようなデータの分布を表した連続的な変数
に関する確率分布である。
中心極限定理により、
独立な多数の因子の和として表される確率変数は正規分布に従う。
このことにより正規分布は統計学や自然科学、
社会科学の様々な場面で複雑な現象を簡単に表すモデルとして用い
られている。
たとえば実験における測定の誤差は正規分布に従って分布すると仮定され、不確かさの評価が計算されている。 また、正規分布の密度関数の
フーリエ変換は再び正規分布の密度関
数になることから、
フーリエ解析および派生した様々な
数学・
物理の理論の体系において、正規分布は基本的な役割を果たしている。
だから、数学の罠、バーチャル、ゲーム => マネークライシス
---Wiki
ナッシュ均衡は、他のプレーヤーの戦略を所与とした場合、どのプレーヤーも自分の戦略を変更することによってより高い利得を得ることができない戦略の組み合わせである。ナッシュ均衡の下では、どのプレーヤーも戦略を変更する誘因を持たない。
そして、計算科学で証明を・・・ NP問題になる
---Wiki
NP完全問題(エヌピーかんぜんもんだい、NP-
complete problem)は、クラス
NP(Non-
deterministic Polynomial)に属する問題でかつ、クラス
NPのすべて
の問題から
多項式時間帰着可能な問題である。すなわち、
NPに属する問題のうちで
NP困難なものである。
クラスNPに含まれる問題で、
あるNP完全問題から多項式時間還元可能なものも、
またNP完全である。
現在発見されているNP完全問題の多くがこの定理によって
充足可能性問題より導かれたものである。
充足可能性問題がNP完全であ
ることは
1971年、
スティーブン・クックによって証明された。
NP困難との違い [編集]
NP困難(NP-hard)には複数の定義があるが、要は「
NPに属する問題と比べ、同等以上に難しい」、
NP以上にハードな問
題という意味である。一方、
NP完全はあくまでNPに属する「
NP
の中では最も難しい」問題なので、
NP困難はNP完全と同等以上に難しい。
つまり難しさで比較した場合
NP≦NP完全≦NP困難である。
定義上、
NP困難である問題は必ずしもNPに属さなくても良いが、
たまたまNPにも属する場合はNP完全と一致する。
一般にNP完全とNP困難は極めて混同されやすく、特に
アルゴリズムを扱う本などでは、
NP完全と表記しながらもNP困難の説明をしていたり、
本来はNP困難ではあってもNP完全ではない問題を「
NP完全の例」として挙げる物が多々ある。
もう一つの理由としてはNP完全とNP困難は
計算複雑性理論の研
究者にとっては重要な違いではあるが、
アルゴリズム論の研究者に
はそれほど重要な違いではないためである。
アルゴリズム論の研究者にとっては
P≠NP予想が肯定されるなら
、どちらも「
多項式時間では解くことのできない問題」
でしかなく、それらの問題に対して
メタ・ヒューリスティックなど
を適用することによってどこまで効率的に近似解を見つけられるか
、多項式時間の内でどこまで小さな
近似度の
近似アルゴリズムを設
計できるかなどが主な論点となり、
両者の違いが大きく出るような状況にはならないからである。
NP完全問題の例 [編集]
---Wiki
(3次元)ポアンカレ予想(Poincaré conjecture)とは、数学(位相幾何学)における予想のひとつ。
ポアンカレ予想とは、
一般化された問題 [編集]
ポアンカレ予想は一般化(高次元に拡張)できる。それは次のようなものである。
このようにポアンカレ予想を
n次元に一般化すると
n=2での成立は古典的な事実であり、
n≥4の場合は早くに証明が得られていた。
n≥5の時は
スティーヴン・スメイルによって(
1960年)、
n=4の時は
マイケル・フリードマンによって(
1981年)証明された。2人とも、その業績から
フィールズ賞を受賞している。スメイルの証明は
微分位相幾何学的なものであったが、フリードマンの証明は純粋に
位相幾何学的なものである。実際、フリードマンの結果はその直後に
ドナルドソンによる
異種4次元
ユークリッド空間(位相的には通常の4次元空間だが、微分構造が異なるもの)の発見へとつながった。以上よりオリジナルである3次元ポアンカレ予想のみを残し、高次元ポアンカレ予想は先に決着してしまった(微分同相については4次元ポアンカレ予想も未解決)。
数学的に厳密ではないが、たとえて言えば、
宇宙の中の任意の一点から長い
ロープを結んだ
ロケットが宇宙を一周して戻ってきて、ロープの両端を引っ張ってロープを全て回収できた場合、宇宙の形は概ね球体(
ドーナツ型のような穴のある形、ではない)と言えるのか、という問題である。
ギャラリー [編集]
自分の体を前後上下無限の間仕切りで真っ二つにしたとき、左から投げた球が宇宙のどこかでいつのまにか間仕切りの右に来ていれば3次元球面に同相とはいえない。 | 有限距離で宇宙にロープを引き回しても、そのロープが無限に回収できなくなる状況の例。無限に細い糸でもやはり回収できないのか? |
3次元ポアンカレ予想と幾何化予想 [編集]
3次元ポアンカレ予想について
ウィリアム・サーストンの
幾何化予想(サーストンのプログラム)があり、これは3次元多様体の分類に関するものである。この予想は3次元ポアンカレ予想を含み、大変壮大なものである。
幾何化予想とペレルマン [編集]
非常に単純に言えば、幾何化予想とは、多様体を8つのピースに分割し、そのピース毎に幾何的性質を調べるというものである。一方で、リッチフローを用いたときに、ピースから全体を構成し直すときに特異点が発生する可能性がある。ペレルマンはこの特異点の発生条件と特異点の性質を調べ、特異点が発生しないような手法を考えた。それが「手術」といわれる方法である。
それ以来ペレルマン論文に対する検証が複数の数学者チームによって試みられた。原論文が理論的に難解でありかつ細部を省略していたため検証作業は難航したが、2006年5 - 7月にかけて3つの数学者チームによる報告論文が出そろった。
これらのチームはどれもペレルマン論文は基本的に正しく致命的誤りはなかったこと、また細部のギャップについてもペレルマンの手法によって修正可能であったという結論で一致した。これらのことから、現在では少なくともポアンカレ予想についてはペレルマンにより解決されたと考えられている。
ほとんどの数学者が
トポロジーを使ってポアンカレ予想を解こうとしたのに対し、ペレルマンは
微分幾何学と
物理学の手法を使って解いてみせた。そのため、解の説明を求められてアメリカの壇上に立ったペレルマンの解説を聞いた数学者たちは、「まず、ポアンカレ予想を解かれたことに落胆し、それがトポロジーではなく微分幾何学を使って解かれたことに落胆し、そして、その解の解説がまったく理解できないことに落胆した」という
[1]。なお、証明には熱量・エントロピーなどの物理的な用語が登場する。
2006年
12月22日、アメリカの科学誌「サイエンス」で科学的成果の年間トップ10が発表され、その第1位に「ポアンカレ予想の解決」が選ばれた
[2][3]。
賞金100万ドル [編集]
アメリカにある
クレイ数学研究所(CMI)はポアンカレ予想を
ミレニアム懸賞問題の一つに指定し、証明した者に100万ドル(約9000万円)の賞金を与えると発表している。ここでペレルマンが本賞を受賞するのかどうかが一部の関心を呼んでいた。また、彼は賞金を受け取る条件である「査読つき専門雑誌への掲載」をしておらずまた彼の証明はあくまでも要領を発表したに過ぎないという説もあった。
CMIの規定では受賞資格者は必ずしも専門誌に掲載された論文の直接的な執筆者に限られる訳ではない。ペレルマンが変則的な発表手段を採り、arXivへの掲載のみに留めて専門誌に投稿していないというそのこと自体は、彼が受賞する上での障害とはならない。CMIは何れにしてもあらゆる素材を吟味して証明の成否を判定し、然る後初めて授賞を検討するようである。
2010年3月18日、クレイ数学研究所はペレルマンへのミレニアム賞授賞を発表した
[4]。これに関してペレルマンは以前、同賞を「受けるかどうかは、授賞を伝えられてから考える」と述べていたが、結局受賞式には出席しなかった。研究所の所長は「選択を尊重する」と声明を発表し、賞金と賞品は保管されるという
[5]。
2010年
7月1日、ペレルマンは賞金の受け取りを最終的に断ったと報じられた。断った理由は複数あり、数学界の決定には不公平があることに対する異議や、ポアンカレ予想の解決に貢献した
リチャード・S・ハミルトンに対する評価が十分ではないことなどを挙げている。さらに、このことについて本人は「理由はいろいろある」と答えた
[6]。

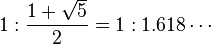 を取る。 これは黄金比と等しい。
を取る。 これは黄金比と等しい。




0 件のコメント:
コメントを投稿